Apprendre dans des situations complexes

Introduire, dès le début d'un apprentissage, les éléments qui permettent à l'élève d'avoir une vue d'ensemble anticipante, c'est une démarche complexe, mais en même temps facilitante.

Tout enseignant a le souci que ses élèves comprennent, lorsqu'il fait une leçon, lorsqu'il introduit une nouvelle notion, lorsqu'il explique, lorsqu'il corrige, etc.; et que ses élèves réussissent lorsqu'ils ont à réaliser une tâche - exercice, problème, recherche etc.
Il peut alors chercher à leur éviter de rencontrer dans un même temps plusieurs problèmes ou plusieurs aspects d' une question, plusieurs manières de faire ou d'expliquer, jugeant que ce pourrait être pour eux, l'occasion de confusions, d'incompréhensions, ou d'approximations. Il peut chercher aussi, par souci d'efficacité, à éviter des risques de divergence entre les élèves de sa classe, craignant que les qualités de persuasion ou la popularité de l'un d'entre eux n'entraîne tous les autres dans des cheminements périlleux, craignant aussi que les erreurs qui pourraient apparaître dans ces circonstances ne se fixent définitivement dans les mémoires.
Le choix pédagogique consiste alors à rendre les plus simples possibles la situation d' apprentissage ou le travail à faire pour faciliter réussite et compréhension.

• D'ordinaire, simplifier la situation d'apprentissage revient à découper l'objet d'étude en unités simples et à distribuer ces unités dans des séances successives. Bien des manuels invitent à faire ainsi : privilégier des explications et des corrections qui vont droit au but : appliquer directement des règles, des procédures canoniques, etc. Il en est souvent de même lorsque l'on simplifie les travaux donnés aux élèves : on ne donne que les informations strictement nécessaires à la tâche ; on pense que toute autre information, non nécessaire, pourrait parasiter la reconnaissance de la situation, empêcher le déclenchement d'un savoir-faire appris et laisser place à un plus grand risque d' erreurs. Tout ceci semble chose naturelle.

• Cependant, tout objet d'étude, tout domaine de contenus est complexe, c'est-à-dire constitué de contenus articulés, en rapports logiques et hiérarchiques les uns avec les autres. Ainsi, par exemple, un texte injonctif 1° est un texte 2° n'est pas un texte argumentatif, ni narratif, ni encyclopédique etc. 3° quoiqu'il puisse être aussi l'un ou l'autre à l' occasion pour certaines de ses parties etc. Ou encore, la symétrie axiale 1° est une transformation géométrique 2° qui s'oppose à d'autres transformations (symétrie centrale, homothétie, translation etc.) conserve comme l'une ou l' autre de ces transformations certaines propriétés des figures.
La question est seulement de savoir si pour les situations d'apprentissage il est préférable de présenter les unités de contenus une par une, ou s'il faut les présenter dès l'abord avec leurs liens logiques et hiérarchiques d'inclusion, de contrariété, de contradiction, etc.

• A cette question, Piaget, il y a cinquante ans déjà, répondait que l'élève ne peut pas apprendre ce qu'on lui enseigne comme on le lui enseigne, s'il ne voit pas l'unité d'où procède le découpage que l'enseignant lui propose. La logique de l'élève n'est d'ailleurs jamais homogène à celle de l'enseignant (ou de l'auteur de manuels), et c'est encore plus vrai lorsque ce dernier simplifie le domaine de contenus en en désarticulant les unités. L'enseignant sait ce qu'il découpe et à quelle place se situent ces simplifications. L'élève, non. Le premier connaît l'unité du domaine de savoir qu'il découpe ; il sait quels sont les liens entre les différentes connaissances et comment elles s'articulent. L'élève, lui, pour autant qu'il est vraiment dans une démarche d'apprentissage, ne se contente jamais de suivre, il cherche à comprendre, à se donner une intelligence de ce qu'on lui enseigne (intelligence = mettre des liens entre). Il a besoin, pour apprendre, de situer son travail actuel dans une perspective plus large, dans une vue d'ensemble anticipante de l'unité de la question à laquelle ce travail participe.
C'est cette vue d'ensemble qui, pour l'élève, donne du sens au travail qu'il fait. Ou sinon, c'est qu'il s'est résigné à apprendre sans comprendre, ce qui n'exclut d'ailleurs pas un certain niveau de réussite, mais limite toujours les possibilités de poursuite approfondie des apprentissages, et même, plus modestement, la capacité à recevoir de l' aide en cas de difficulté.
Ce que nous désignons par complexité dans le champ de l'apprentissage, c'est donc le respect des liens «naturels» qui organisent un domaine de connaissances. Il s'agit d'introduire dès le début de l'apprentissage les éléments qui permettent à l'élève d'avoir une vue d'ensemble anticipante, déjà parente de la connaissance qu'a l'expert du domaine de contenus. Ce respect des liens favorise les représentations unifiantes, intelligentes, des objets d'apprentissage, et facilite la circulation de l'esprit le long des liens: il favorise l' intelligence, la puissance d' établir des liens.

Richard Assuied et Anne-Marie Ragot ont participé à la recherche sur l'école maternelle bilingue en Vallée d'Aoste, aspects psycholinguistiques et psychopédagogiques (1994) et sont les auteurs de la recherche sur l'évaluation des compétences cognitives des élèves en situation bilingue à la fin de l'école moyenne (1999).

Travailler en ayant le souci de la complexité:

• c'est être au plus près du fonctionnement cognitif de l' élève, puisque lui-même, pour comprendre, cherche à établir des liens;

• en respectant les liens internes au domaine de contenus, c'est contribuer au travail de mémorisation, à l'organisation en mémoire à long terme, et orienter le fonctionnement de la mémoire (analyse des situations nouvelles et transfert);

• c'est pouvoir tirer profit des connaissances et des ressources cognitives présentes dans le groupe-classe (maître et élèves), en prenant appui sur les interactions dans la classe (observer, réfléchir, faire des remarques, discuter, essayer...).

Ces interactions trouvent dans la complexité des objets d'étude l' occasion de leur émergence et de leur rebond.

• En pédagogie, cette orientation se met en oeuvre à travers deux grandes formes de situations : les situations-problèmes et les situations de catégorisation, généralisation, définition. Mais elle peut être aussi largement présente dans les activités ordinaires de la classe.

Les situations-problèmes

Les situations-problèmes introduisent des apprentissages à visée théorique.
Leur objectif est de permettre la construction par l'élève d'une conduite cognitive nouvelle, c'est-à-dire d'une connaissance et d'un «mode général d'action» qui vont rendre possible, par la suite, la résolution d'une classe de problèmes donnée.
En situation - problème, ce n'est donc pas seulement la résolution d'un problème singulier qui est recherchée, mais, à travers elle, la capacité à analyser une situation du point de vue de son contenu et de sa structure, la capacité à reconnaître une situation ou un objet comme constitués d'un ensemble de relations, donc d'une certaine façon la capacité à reconstruire l'objet étudié pour en examiner les principes structuraux, formels.
Prenons pour exemple la situation-problème classique suivante : on veut agrandir cette figure sans changer sa forme. On a commencé à transformer le segment AB. Continue.

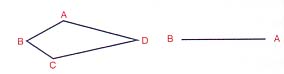
• Il ne s'agit pas seulement de parvenir par tâtonnements, essais et erreurs, à obtenir une figure plus grande.
Mais la résolution de ce problème, l'examen des difficultés qu'elle pose à l'élève, des erreurs qu'elle engendre, permet de dégager l'ensemble des traits par lesquels se définit ce type de transformation et leur unité : conservation de la forme et conservation du nombre de côtés et conservation des angles et application d'un coefficient de proportionnalité, le même pour tous les segments et conservation des rapports internes à la figure (AB/BC = A' B' /B' C') ; il permet aussi de dégager l'ensemble des opérations numériques utilisables (multiplier par un nombre entier, un nombre décimal, une fraction), et le lien entre l'opération numérique choisie et son effet géométrique ; il permet encore de dégager une procédure géométrique possible (théorème de Thalès) ou encore les transformations de périmètre et d'aire introduites par la transformation géométrique et le lien entre ces transformations et le coefficient de proportionnalité, etc.
Du point de vue des conduites cognitives générales, cette situation suppose encore comparaison et analyse des données (quelle est la différence de mesure entre les segments AB en A' B' ? Par quelle opération numérique peut-on passer de la première mesure à la seconde ?) anticipation et planification (comment continuer ? à quoi faire attention ? ), contrôle (la procédure que j'utilise conserve-t-elle bien la forme ?) etc.
Il ne s'agit donc pas de s'intéresser seulement à la figure donnée, et de réussir à la transformer, mais, grâce à elle, d'examiner les aspects structuraux des figures géométriques et de définir les propriétés de cette transformation.
Ce que cette situation permet de construire chez l'élève, c' est l'intelligence du concept de figure géométrique comme ensemble de propriétés, et l'intelligence des effets de cette opération de transformation sur l'ensemble des propriétés de la figure ; intelligence que viendra nommer le concept d'homothétie. Il reste ensuite à vérifier si ce que l'on a formalisé pour l'agrandissement vaut aussi pour la réduction, à proposer ou à faire créer par les élèves toute une série de problèmes pratiques, concrets, à résoudre, et enfin à produire des énoncés généraux et mémorisés.
A l'issue de cette séquence d'apprentissage l'élève peut alors disposer d'un nouveau «savoir théorique» généralisable et applicable à une classe de problèmes.
On le voit dans cet exemple, une situation problème n'est pas obligatoirement une situation compliquée, imposant le traitement d'une profusion d'informations. Le caractère complexe ne porte pas sur la mise en relation de toutes sortes d'informations dispersées. Il porte sur l'exploration, la mise à jour et l'analyse des liens internes à l'objet d' étude.
Il n'y a apprentissage par résolution de problème (problem solving) que si le sujet qui apprend «problématise» la situation, c'est-à-dire extrait, démêle, analyse et formalise les liens qui la constituent.

• Pour poursuivre cet objectif de construction de savoir théorique, les situations-problèmes confrontent les élèves à des questions, pour lesquelles ils ne disposent ni de règle permettant une décision adaptée, ni de procédure canonique de résolution.

• Dans l'apprentissage en situation-problème :
- les élèves commencent à travailler en s'appuyant sur leurs connaissances actuelles. La situation-problème permet aux élèves de commencer à travailler avec ce qu'ils savent. C'est le premier facteur de facilitation de l'apprentissage : les connaissances auxquelles la question est rattachée sont identifiées de façon explicite.

• Il va donc être plus aisé pour les élèves de prendre conscience des limites de ces connaissances, de remettre en question les représentations du problème qu'ils ont construites en s'appuyant sur elles, de chercher d'autres possibilités d'aborder la question.
Les élèves se représentent alors ce qu'ils ont à apprendre précisément comme étant un problème, c'est-à-dire quelque chose d'irréductible à une simple démarche de reconnaissance, ou à une résolution strictement adaptative, pragmatique.

• Il va être également plus aisé pour l'enseignant d'ajuster la situation d'apprentissage, en y introduisant des conditions (variables didactiques) qui rendent impossibles certaines tentatives de résolution et obligent les élèves à transformer ou abandonner les connaissances auxquelles ils se réfèrent, pour inventer d'autres solutions : il ne s'agit plus de faire avec ce qu'on sait, mais de faire avec ce qui fait que l'on ne sait pas. Chacun, élève et enseignant, sait alors clairement sur quelles connaissances il peut compter et lesquelles doivent être abandonnées.

• A l'inverse, si les connaissances avec lesquelles les élèves accueillent un problème ne sont pas identifiées, elles peuvent constituer des obstacles ou des points de résistance à l'apprentissage (pourquoi apprendre si on a l'impression de savoir déjà faire?).
- Il s'agit de donner aux élèves les moyens de construire un savoir, le même pour tous, en prenant appui sur le fait que les connaissances actuelles évoquées par chacun different d'un élève à l'autre. La situation-problème permet l'approche de la question à partir de points de vue différents. Ce sont donc autant de représentations de la situation, autant de procédures, que les élèves vont comparer, discuter, évaluer, coordonner, dans une activité de résolution conjointe du problème.
L'apprentissage dans des situations de complexité ne peut jamais être affaire purement individuelle. Il rend nécessaires les interactions, sous les deux modes de la confrontation et de la coopération.
C'est la confrontation des points de vue, la comparaison des propositions qui permet à chacun de douter de sa propre idée, de remettre en question sa représentation, qui permet à tous de coordonner leurs actions pour faire évoluer les procédures utilisées, de converger dans une attention plus fine, plus analytique à l' objet d' étude.

Là encore on trouve des facteurs de facilitation :

• l'obligation d'expliciter pour pouvoir être compris des autres oblige chacun à objectiver ses propres pensées, à les mettre en forme justifiée, logicisée, et pas seulement «comprise» en gros pour et par lui-même ; il doit transformer des choix en procédures exprimables, descriptibles, ce qui suppose un puissant effort d' explicitation, de logicisation, de formalisation ;

• l'obligation de discuter les solutions de façon argumentée, de réfléchir sur les limites des connaissances auxquelles on se réfère, contribue à mettre en place la structuration logique des contenus ; les oppositions de points de vue engagent une résolution des problèmes à un niveau logique supérieur à ce que chaque élève pourrait comprendre seul, ou à ce qu'il pourrait comprendre si le maître seul exposait les solutions.
Cette discussion prépare ainsi l'évolution vers la formulation de procédures plus «canoniques», c'est-à-dire plus rapides, plus directes, plus efficaces, plus élégantes, après examen comparatif de différentes stratégies moins performantes ;

• dans ces interactions, chaque élève tire bénéfice des paraphrases, reformulations, idées neuves, qu'apportent les autres élèves pour transformer son point de vue, faire évoluer sa propre représentation, inventer d'autres solutions. La dynamique des interactions et sa fécondité pour l'apprentissage est donc très sensible à la façon dont l'enseignant organise la discussion, choisit les productions, objets de confrontation, met en relation des élèves auteurs de points de vue différents ; elle est très sensible à la façon dont il donne aux élèves la possibilité d'aller au plus loin dans leur approche propre, et dans la rencontre avec les approches des autres.
- Les formulations conclusives s'inscrivent dans la continuité des échanges langagiers. Elles sont ainsi proches des capacités énonciatives des élèves et acceptent elles aussi la variation.
Ainsi conçues, elles favorisent un encodage plus sûr et souple des notions en mémoire à long terme, qui s'oppose à l'apprentissage par coeur et permet aux connaissances d'être évoquées de façon efficace dans des situations nouvelles.
A titre d' exemple voici un recueil de formulations d' élèves de 3^ème année de l'école élémentaire à l' issue d'une situation-problème destinée à faire travailler les liens entre numération, addition et multiplication par dix : ces formulations sont toutes issues des remarques et discussions qui ont accompagné les différents moments de la situation-problème.
Elles ont été, séance après séance, notées et conservées, puis rediscutées.
Leur validation elle-même a fait l' objet d' un travail conduit de façon stricte par l'enseignante ; elles ont été déclarées exactes et équivalentes et font dorénavant partie du répertoire de références et de règles de la classe.
- Multiplier par 10 c' est facile ; - on remarque que toutes les fois qu'on multiplie un nombre par 10, on écrit un 0 à droite de ce nombre ; - pour multiplier par 10, on n'a pas besoin de poser une opération; - quand on multiplie un nombre par 10, ce nombre devient un nombre de dizaines. On n'a plus qu'à écrire un 0 à la place des unités ; - multiplier par 10, c'est plus rapide que faire une addition avec dix fois le même nombre.

• En quoi le fait de disposer d' une telle variété de formulations est-il aidant?

• Chacun peut mettre en mémoire l'énoncé à travers lequel il reconnaît le mieux ce qu'il sait. Chacun sait aussi qu'il a d'autres énoncés à sa disposition et qu'il peut également les mémoriser ou y revenir en cas de besoin ;

• Mais surtout, chacun de ces énoncés peut être particulièrement adapté à une situation de rappel. Ainsi, la première formulation peut être suffisante pour mettre en place une procédure automatisée en calcul mental ; la seconde et la troisième en calcul écrit ; la quatrième lorsqu'il s'agit de distinguer chiffre des dizaines et nombre de dizaines, ou de remplir un tableau de numération ou de conversion.

• A l'issue de cette situation d'apprentissage, les élèves étaient devenus très curieux des propriétés de la numération.
Au point que, lors de la dernière séance, un certain nombre d'élèves, poursuivant la recherche de liens entre les nombres et les opérations, ont eu l'intuition que tous les nombres entiers peuvent être conçus comme des multiples de 10, anticipant de cette façon l' existence des décimaux.
L'enseignante a confirmé cette idée, tout en renvoyant les élèves à plus tard dans leur scolarité.
La situation-problème, en mettant au travail les capacités d'analyse et de raisonnement des élèves et en les développant, peut ainsi les engager à envisager l'extension et le remaniement de leurs connaissances et faire de l'apprentissage une histoire... à suivre !

Anne-Marie Ragot - Richard Assuied
Agrégés de philosophie et diplômés de troisième cycle de psychopathologie clinique.
Professeurs à l' Institut Universitaire de Formation de Maîtres, Saint-Germain-en-Laye, où ils enseignent la psychologie de l'enfant et la psychologie des apprentissages.
Anne-Marie Ragot, en outre, a travaillé comme chercheur en didactique à l'Istitut National de la Recherche Pédagogique.