Le trasformazioni geometriche in matematica e fisica
Il percorso didattico, elaborato grazie al lavoro di collaborazione di due insegnanti, verte sull'insegnamento delle trasformazioni geometriche in matematica e fisica nel triennio del liceo scientifico. L'attività viene svolta proseguendo la trattazione sintetica ed empirico-sperimentale già avviata nel biennio.
Nel presentare
la nostra proposta ci sembra importante definirne i contenuti nell'ambito
della didattica vista come problema complesso. Non vi è dubbio,
infatti, che il problema dell'insegnare non sia né un problema
semplice né un problema complicato suddivisibile in problemi semplici,
ma è un problema complesso difficilmente scomponibile.
Ogni argomento, oggetto della trasmissione del sapere, è inserito
in diversi contesti di conoscenza e con questi è strettamente intrecciato.
Il tema delle trasformazioni geometriche del piano, in particolare nei
Licei Scientifici, è un esempio di sapere intrecciato che offre
notevoli spunti interdisciplinari, in particolare con la fisica, e ben
si presta ad essere affrontato secondo un percorso a spirale.
La nostra proposta si riferisce all'insegnamento delle trasformazioni
geometriche in matematica e fisica. Tale percorso, schematico dal punto
di vista analitico, viene svolto nel triennio, proseguendo la trattazione
sintetica ed empirico-sperimentale già avviata nel biennio.
Il lavoro svolto nelle nostre classi relativamente all'insegnamento delle
trasformazioni geometriche del piano in sé permette di passare
via via dall'isometria, alla dilatazione, all'omotetia e, per finire,
alla similitudine e alle affinità.
Il percorso descritto non può prescindere dall'ordine sequenziale
con il quale è presentato in classe. Ci sembra molto efficace,
però, procedere seguendo un andamento a spirale, coinvolgendo anche
la Fisica, ampliando e approfondendo quindi argomenti già trattati
in modo da muoversi sempre più in direzione di maggior formalizzazione
e astrazione.
In terza liceo si introduce il piano cartesiano e la Geometria Analitica
partendo dalla rappresentazione dei punti, analizzando le loro proprietà
legate alle coordinate e associando ad essi il concetto di funzione.
Le trasformazioni del piano in sé, in particolare le simmetrie
assiali e centrali rispetto agli assi di riferimento, si possono introdurre
come estensione analitica delle conoscenze di geometria euclidea, già
consolidate nel biennio, e procedere fino a giungere alle equazioni che
esplicitano tale relazione anche in ambito algebrico. Il piano euclideo
in realtà giace sempre sotto al piano cartesiano e ne costituisce
un sottoinsieme metrico: la geometria e le proprietà delle figure
non variano, sempre in un'ottica di continuità con il biennio.
Si possono proporre esempi di vario tipo, tra questi il seguente:
Dato un punto disegnato nel piano a caso, si introduce il sistema di
riferimento e si associano ad esso le coordinate come distanze relative
dagli assi; successivamente si chiede agli studenti di disegnarne i simmetrici
rispetto agli assi cartesiani e rispetto all'origine e di individuarne
le coordinate; infine di ipotizzare le relazioni tra le coordinate del
punto dato e quelle dei suoi trasformati.
Questo procedimento potrà essere ripreso in quarta quando, in goniometria,
si introducono gli angoli associati: le relazioni tra le funzioni goniometriche
di questi e degli associati dei complementari sono immediatamente riconosciute
se legate alle simmetrie.
Quando, sempre in terza, il concetto di funzione sarà proposto
come relazione tra numeri reali, quindi come relazione tra punti appartenenti
alla retta reale, e il suo grafico come una possibile rappresentazione
del prodotto cartesiano RxR, si possono ricavare le proprietà di
parità, disparità e invertibilità delle funzioni
analizzando particolari simmetrie.
Una funzione è pari se e solo se f(-x) = f(x) ma anche se il suo
grafico è simmetrico rispetto all'asse delle ordinate; così
come la simmetria rispetto all'origine rivela che la funzione è
dispari. Se una funzione è invertibile il grafico dell’inversa
si ottiene per simmetria rispetto alla bisettrice del I e III quadrante.
Utilizzando le simmetrie dei grafici rispetto agli assi coordinati si
introduce abbastanza agevolmente il significato di valore assoluto ed
è possibile arrivare graficamente alla rappresentazione di |f(x)|
e di f(|x|) trasformando quello di f(x).
L'argomento può essere completato dimostrando che una simmetria
è una particolare isometria, una trasformazione cioè che
mantiene le distanze: per esempio fornendo le coordinate di due punti
si chiede di verificare che la loro distanza coincida con quella dei loro
simmetrici le cui coordinate devono essere trovate algebricamente applicando
le equazioni della trasformazione.
Considerato il numero limitato di ore a disposizione in fisica, visto
il buon bagaglio in geometria, è necessario applicare al massimo
il concetto di modello matematico per permettere agli studenti di utilizzare
le stesse relazioni viste in matematica nello studio di fenomeni, anche
se caratterizzati da grandezze fisiche diverse.
Quando si affronta l'equilibrio si possono trovare le coordinate del baricentro
di un corpo omogeneo piano e regolare. È possibile far sì
che gli studenti stessi riescano da soli ad intuire come le simmetrie
viste all'inizio dell'anno scolastico conducano ad approfondimenti e riflessioni
nella statica dei corpi non vincolati.
Nell’ambito delle prime lezioni di fisica si incontrano i concetti
di riduzione in scala delle misure, di proporzionalità diretta
e inversa tra grandezze, argomenti che possono introdurre il concetto
di dilatazione e di omotetia da svolgere in quarta. Persino la modifica
di una finestra di dialogo in Windows è un'ottima occasione per
introdurre il concetto di glissosimmetria e di dilatazione.
Proponendo differenti grafici di funzioni dilatate sia in orizzontale
sia in verticale appare chiaro come sia possibile ricavare le equazioni
della dilatazione partendo dall’osservazione diretta del piano cartesiano.
Allo stesso risultato, anche se in maniera più empirica, si giunge
attraverso il confronto diretto di rappresentazioni tabellari.
Si possono proporre, sfruttando un foglio di calcolo, le rappresentazioni
di y=sen(hx) e y=ksenx e la loro composizione y=ksen(hx). È possibile,
poi, confrontare le tabelle dei loro valori, ricavando importanti proprietà
del grafico: non variano le intersezioni con l'asse perpendicolare alla
dilatazione, la pendenza del grafico trasformato aumenta, la dilatazione
su y è proporzionale al fattore di proporzionalità indicato
dal parametro k mentre su x è inversamente proporzionale al parametro
h.
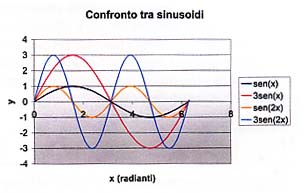
Diventa naturale
il legame con le equazioni dei moti armonici e delle onde: la dilatazione
orizzontale è legata alla frequenza dell'onda, quella verticale
all'ampiezza dell'oscillazione.
In quarta, infine, si studia la geometria solida euclidea e in particolare
il principio di Cavalieri per il confronto dei volumi dei solidi: l'omotetia
e i rapporti ben si prestano ad interpretare le figure solide e a risolvere
i problemi per via sintetica.
La fisica della classe terza offre tre notevoli spunti come approfondimenti
delle traslazioni:
1) i vettori e le loro componenti;
2) lo studio del moto relativo con le trasformazioni galileiane;
3) la legge dei gas perfetti con t=T+273.15.
In tutti questi casi, seguendo l'evoluzione storica dei concetti e sfruttando
ciò che gli studenti già conoscono sulle traslazioni, è
spontanea la discussione e la nascita delle equazioni delle trasformazioni
che in fisica hanno un concreto significato e che, talvolta, non sono
né semplici da introdurre né di facile assimilazione.
In quarta, generalmente nel secondo quadrimestre, si studia anche l'ottica
ed è particolarmente ben riuscito il collegamento tra proiezioni,
omotetie e la generazione delle ombre per giustificare: la propagazione
rettilinea della luce, la legge dell'irraggiamento (proporzionalità
con 1/m2), le eclissi con
un'appendice all'astronomia, senza contare l'importanza che hanno, nel
corso di disegno, la rappresentazione in scala, le proiezioni ortogonali
e lo studio delle ombre, argomenti che offrono spunti per approfondimenti
multidisciplinari.
È noto dallo studio precedente, se non lo è questa è
un'ottima occasione per spiegarlo, che ogni isometria si può pensare
come composizione di al più tre simmetrie assiali; sfruttando le
simmetrie e la composizione di funzioni si può quindi passare alla
traslazione o alla rotazione.
Generalmente la traslazione è argomento di terza mentre la rotazione
è affrontata in quarta per il suo legame alla goniometria.
Le coniche in quarta vengono affrontate grazie a traslazioni. Gli studenti
vengono invitati a riconoscere la conica e, attraverso il completamento
del quadrato, ottenerne l'equazione canonica traslata. In quarta, grazie
ai primi elementi di goniometria, è possibile cercare le equazioni
delle rotazioni.
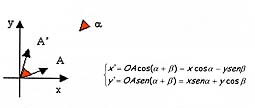
È utile
applicare dapprima il sistema di equazioni alle coordinate dei vertici
di un triangolo qualunque. Il triangolo ABC e il suo trasformato A'B'C',
disegnati nello stesso S.R. permetteranno di individuare con chiarezza
l'angolo a di rotazione.
Le equazioni delle rototraslazioni:
![]()
saranno, infine, determinate a partire dagli stessi studenti, grazie alle
capacità di astrazione ormai acquisite.
La naturale applicazione del lavoro svolto fin qui in geometria analitica
è l'applicazione delle coniche rototraslate in Astronomia. Proponiamo
nel box il lavoro descritto come "L'orbita dell'EXPLORER 35".
Tale attività ha permesso di intrecciare la matematica e la fisica
in maniera particolarmente efficace. Tale esperienza viene generalmente
affrontata dai ragazzi in maniera entusiastica, probabilmente perché
gli studenti si rendono conto di essere parte attiva nella costruzione
del loro sapere. Grazie alle proprietà dell'ellisse, alle leggi
di Keplero, alla legge di gravitazione universale e, non ultimo, al foglio
elettronico, l'importanza del modello matematico, più volte sottolineata,
assume caratteristiche reali e gli allievi ne percepiscono completamente
l'importanza.
CONCLUSIONI
A questo punto l'essenziale è stato presentato, ma non esaurisce certo l'argomento delle trasformazioni geometriche. Nel corso dei tre anni, gli studenti hanno modo di applicare ciò che hanno studiato, sono in grado di riconoscere alcuni invarianti per le trasformazioni, riconoscono il metodo scientifico e sono autonomi nel procedere. Il grado di soddisfazione è buono sia per i docenti coinvolti sia per gli allievi che sono consapevoli dei progressi da loro compiuti.
Mappa concettuale percorso proposto
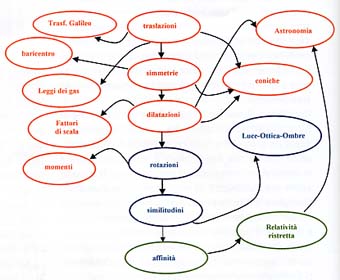
Legenda:
classe terza, classe
quarta, classe
quinta
Marina Villani
Orianna Cremonese
Insegnanti di Matematica e Fisica
press il Liceo scientifico di Aosta
Bibliografia
AMALDI U., La fisica per i Licei Scientifici, Vol. 1, 2, 3, 1998, Zanichelli,
Bologna
ORIOLO P., CODA A., Matematica, Vol.2, 1996, ed. Scolastiche Mondatori,
Milano
BATTIMELLI G., STILLI, R., Le vie della fisica, Vol.2, 1998, Laterza,
Roma-Bari
Piccato A., Dizionario dei termini matematici, 1987, Rizzoli, Milano
Glossario OMOTETIA: (dal
greco homós, uguale, e thetós, collocato). Due figure
si dicono omotetiche se si corrispondono punto per punto in modo
tale che le rette congiungenti due punti corrispondenti AA', BB'...
passano tutte per un punto fisso O, detto centro, od origine, dell'omotetia;
le distanze da due punti qualunque corrispondenti, od omologhi,
hanno rapporto costante k, detto rapporto di omotetia. GLISSOSIMMETRIA: (dal francese glisser, sorrere, scivolare, e simmetria, dunque simmetria scorrevole). È il prodotto di tre particolari simmetrie assiali. I tre assi delle simmetrie m, n, l sono tali che m è diversa da n e m e n sono perpendicolari a l. Il prodotto è commutativo. La retta l è la direttrice della glissosimmetria ed è l'unica retta unita. LEGGE DELL'IRRAGGIAMENTO: È la legge che spiega come varia l'energia proveniente da una sorgente luminosa al variare della distanza dalla sorgente. Si verifica che tale energia è proporzionale a 1/r2. |
Esempio di applicazione della traslazione nella fisica dei gas perfetti Problema:
cerchiamo la legge che mette in relazione i parametri di un gas
perfetto. |
Esempio di applicazione delle trasformazioni con le coniche
|
Esempio di applicazione delle trasformazioni sempre con le coniche ma in Fisica L'orbita dell'Explorer
35 verifica delle leggi di Keplero Verifica se l'orbita è in accordo con la prima legge di Keplero e con la seconda legge di Keplero. Suggerimenti: Osservazioni:
|
Problema:
Data una piramide di altezza h, determinare a quale distanza x dal
vertice bisogna condurre un piano parallelo al piano della base
in modo che la piramide resti divisa in due parti uguali.
detto h/x il rapporto omotetico, si otterrà:
dove BC e B'C' sono le lunghezze di spigoli omologhi delle basi. Si ottiene infine:
Il rapporto omotetico consente, dunque, una rapida ed elegante soluzione del problema proposto. |

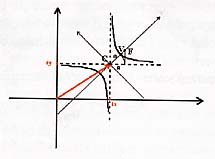 Supponendo
che gli allievi già conoscano la legge di proporzionalità
inversa xy = k e la sua rappresentazione cartesiana:
Supponendo
che gli allievi già conoscano la legge di proporzionalità
inversa xy = k e la sua rappresentazione cartesiana: